
So, way back when, I was browsing the internet and came across r/SpeedOfLobsters. This community survives off of blacking out certain letters in the text of a meme or image to create another word / sentence. An example (from here) is shown below:

Another community I frequent is Code Golf, where people come up with interesting problems and try to solve them using programs with imposed constraints, for example display 2014 without any numbers in your source code, or output Hello, World! with the shortest code possible. As you might expect, several programming languages have been invented specifically for these types of challenges - the language Stuck will print Hello, World! with an empty program! One of the challenges of a problem, therefore, is trying to keep it “odd” enough that it still presents a tangible difficulty to these golfing languages, and yet is simple enough to be interesting.
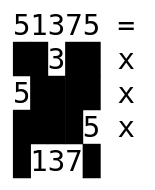
I realized that the SpeedOfLobsters idea of blacking out portions of words could work with numbers and their factors. That is, starting with a number, could you black out some of its digits to leave just one of its factors, for every single factor? After making a basic progam in Python to verify that such numbers existed, I submitted the question and I think it was successful. The Jelly answer, for instance, required a whole 10 bytes! It also prompted some further thought - Carl Witthoft ended up asking a question on mathoverflow on what I ended up terming the “strong” variant, where each digit is used only for a single factor’s subsequence.
A “Lobster Number” is a composite number n such that all prime factors of n are a subsequence of n
< what does this mean in simple terms? >
There is also a “strong” variant, for which I have yet to find an example:
A “Strong Lobster Number” is a composite number n such that all prime factors of n are a subsequence of n, and each digit of the number is a member of at most one subsequence
In actuality, each digit would have to be a member of exactly one subsequence, because of the following: 9 x 9 results in two digits (81). Even 9999 x 9999 will still only result in 8 digits (99980001). In order for a number to have more digits than all its factors combined, a single digit would have to be more than 10, which is impossible. It is, however, possible to have fewer digits (i.e. 1 x 1 results in one digit (1)). However, to satisfy the strong lobster constraint, a number has to have at least as many digits as its factors, or a single digit would have to be used more than once. Therefore, the second part of the definition could be worded
… each digit of the number is a member of exactly one subsequence
without any effective difference.
First, take a composite number and a list of primes up to the square root of the number. Try to divide the number by each prime in ascending order. Once you find a factor, start again from the beginning of the list with the resulting number. When the resulting number is itself prime (which is determined if none of the numbers in the list can factor the resulting number) your list is complete. Now, for each factor, see if its digits can be found in the original number. If all factors can be found in the number then it is a lobster number. There are some optimizations that can be had (like in checking each factor as it is found), but in general finding lobster numbers is a matter of iterative searching.
There are many lobster numbers, starting with 25, 32, 121, 125, 128, 135, 175, 243... you’re only up to 312759 as the 1000th. (There is a file here if you want to see more). However, none of these are strong, because at least one of the digits has to be used more than once. For example, 25 = 5 x 5, so the 5 is used twice, and 32 = 2 x 2 x 2 x 2 x 2, so the 2 is used five times. It makes sense to try to find this programmatically, and in fact it is quite simple due to the way the definition can be expressed. If each digit of the number is a member of exactly one subsequence, then all you have to do to find if a lobster number could be strong or not is take the number, and concatenate the list of its factors. Sort each from smallest to largest digit. If the two resulting numbers are equal, then it could be a strong lobster number. In practice, the remaining examination can be done by hand, as the number of these candidates is quite low. For numbers less than 2^31, the following candidates exist:
Candidate Prime Factors
116191021 [1901, 61121]
137007319 [3701, 37019]
139721397 [3, 71, 71, 9239]
178523471 [7, 41, 73, 8521]
1025460301 [4001, 256301]
1160910031 [19031, 61001]
1167139021 [7121, 163901]
1178677319 [31, 61, 71, 8779]
1195619071 [6101, 195971]
1302480481 [401, 3248081]
1365161273 [7, 61, 523, 6113]
Oddly enough, they all start with 1, but unfortunately none of them are actually strong lobster numbers. This can be simply seen by looking at the numbers of factors with leading ones, which is always less than the number of leading ones. If anyone finds an example of a strong lobster number, they are welcome to contact me directly or to leave an answer / comment containing the number and how they found it at Carl Witthoft’s question on mathoverflow.